When I went to the Alumni Weekend at UC Santa Cruz this year (2017), I came across a curious coincidence.  I signed up to see a show about artificial coral reefs made by crochet.  It looked colorful and fun, so I went.

Little was I prepared for what I encountered upon entering the exhibit.  The show, made by two Australian women (Margaret and Christine Wertheim), was displayed in the smallest space it had yet been in (it is a widely popular international exhibit, but the Mary Porter Sesnon Gallery is small).  This made for a wonderful over-load of form and color, and you immediately knew something different was going on here.  Then I read the introductory explanation at the beginning (stenciled on the wall, as is the custom), and I immediately sought a brochure.  As the brochure didn’t have all the information in the introduction, I took some quick notes, written on the brochure.

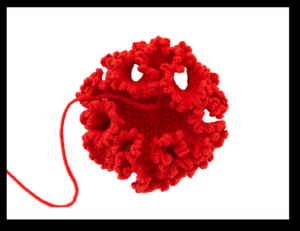
Why does crochet make such natural coral patterns?  The answer is “hyperbolic geometry.”  The “algorithmic codes of crochet” create the “undulating structures of corals” and are a “handicraft parallel to DNA.”  This was first demonstrated mathematically by Dr. Daina Taimina of Cornell University in 1997.  Given a simple one-one crochet pattern, and you get a spiral.  The first display in the show shows two spirals paired up to form a double helix.

From that basis, variations in pattern and material burst forth in a dizzying array of 3-D patterns.  Instead of 1:1, one can do 1:2; instead of silk string one can use fuzzy twine.  The exhibit also informed visitors that many life forms share this type of math, notably cabbages.  Why cabbages?  Well, their form is what is called “crenellated,” which means that they fold back on themselves multiple times in multiple directions, allowing the plant to increase its surface area considerably while maintaining a limited volume.  It is the patterns used by castle fortifications to provide multiple angles and levels of attack by bowmen and other defenders, as seen here:

So much of life involves creating and maintaining increasing surface area in limited volumes.  In fact, our image of DNA is deceptive in this regard, as what we usually see is a straightened out depiction.  DNA is not only two strands coiling around each other — the coils themselves are coiled in order to achieve limited space to operate within the cell.

So my imagination was doing a virtual crochet job with this information when the Curator gave a presentation.  As she spoke I started to add comments which quickened the pace of interest of the small group.  What I realized on the spot was that the difference between Euclidian Geometry (EG) and Hyperbolic Geometry (HG) is that Euclidian is one-handed (typically right-handed) and Hyperbolic is two-handed (the back and forth of crochet).  A series of associations was generated by this observation:  1)  EG is bound by the Cartesian Grid, which typically goes from left to right (X axis) and bottom to top (Y axis), whereas HG can go in any or all directions (together or separately); 2)  EG is straight lines, whereas HG is curved lines (they can be straight if they have zero curvature); EG can only go in one direction at a time, whereas HG typically goes in two directions at once; 3) EG is abstract and can be lain over reality to outline the two-dimensional profile of a 3D reality, whereas HG is embodied by the very back and forth process that creates it (more or less pull in this direction or that, an added stitch or a dropped stitch here or there — it is crafty rather than mechanical).

Afterwards the Curator asked me about my interest, informing me that this show was part of an inter-disciplinary effort between the Arts and Sciences.  She asked me if I was aware of Ren Weschler’s new book on planetary patterns, and I let her know that I had the good fortune to be a special guest at his presentation at UCSC the previous month.  I briefly explained my work on developmental psychology and gave her my card.  She said she would be interested in my presentation as part of their theme.  I told her I was in contact with the Provost of Cowell College.

That very evening I was dining with the loyal critic of my project, Dr. Saposnek.  It turns out one of his wife’s many talents is crochet.  She had heard about the show and they were excited to be able to see it before it left Santa Cruz.  The show and the women who created it have developed an international following of crochet groups, teaching more and more people.  Another aspect of the show I can’t fail to mention is the depictions of the effects of pollution on the coral reef, with plastic and waste suffocating and bleaching the coral.  This indeed can be an apt metaphor for the pollution of our children’s and peers’ development when we are being stuffed with plastic, junk food, and video-tape (yes, discarded video tape is a major polluter of the reef, and when it gets entwined with the coral and it gets twisted by the currents, it develops a diabolically beautiful display that only crochet artists could so vividly depict).

 

 

 

 

 

 

 

Apparently hyperbolic geometry travels up and down the coast, as my friends from Santa Cruz found the necklace below on a trip to Morro Bay.  The glass bead double-helix structure is crafted by Mayan women in Guatemala:

 

There is a similar analogy between lady bug wings and origami.  Slow motion photography and science has found that lady bug wings unfurl like origami creations where layers of paper folded in different directions creates different dynamics.  The following video shows the slow-motion unfurling of the lady bug wings and how it is like origami.

 

 

 

 

 

 

 

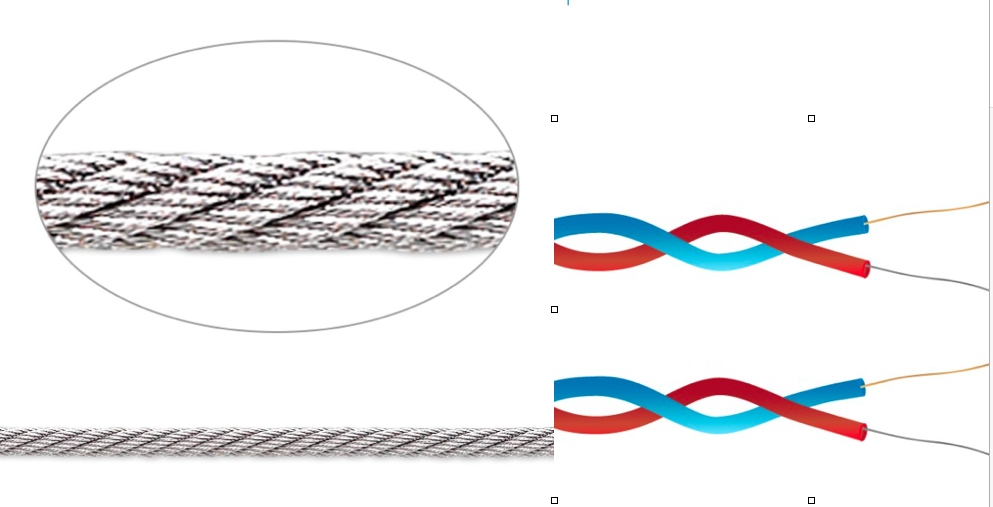
Beading wire, which needs to be very thin and strong, and electric cables, which need to conduct electricity with efficiency, use coiling to enhance their strength and speed.  These have double-helix type structures, as can be seen in these images:

All of this adds up to a perspective that Euclidean Geometry is the mathematics of mechanics, while Hyperbolic Geometry is the mathematics of organics.  In other words, angles are true to machines, while curves are true to life.  Indeed, HG could be called the geometry of growth, while EG could be called the geometry of targeting.  NASA scientists didn’t need mathematics beyond Newtonian Calculus to land the Mars Rover (quite the target practice!), but such pinpoint precision doesn’t capture the dynamics of growth.  To kill it, you need to pin it down; to help it grow, you need to open your arms, both sides, hyperbolically.

The relationship between organics and mechanics has an anthropological background that was pointed out to me by my thesis sponsor Bhuwan Lal Joshi.  He used pattern recognition to determine that many of human’s mechanical inventions have been inspired by organic patterns.  For instance, the pattern of the wheel, a human invention possibly only second to language and writing, can clearly be seen in natural objects such as the orange.  Cut an orange across the equator, and you will find an axle in the center, spokes radiating out from the center, a rim in the form of a rind, and a tire in the form of a peel.  Or vice-versa.  This makes hyperbolic geometry the basis, and Euclidian geometry the derivative.

 

[Of course, logs were the original “wheels” used to transport heavy stones such as those used to build the pyramids of Egypt. But logs are not efficient at transporting people (other than Fred Flintstone).]

 

 

 

 

Another example of hyperbolic geometry has been recently discovered with the unique growth patterns of Cook Pines.  In both hemispheres of the planet, Cook Pines lean towards the equator.  This has been determined to be a phototropic effect, the trees leaning towards the sun.  In this way, Cook Pines simultaneously grow against gravity and towards the sun  (like how sunflowers turn towards the sun). This demonstrates that the law of attraction (sun-loving) can exist side-by-side with the law of compulsion (gravity-resisting).

 

 

 

 

 

 

 

 

 

 

Now let us consider some ways in which hyperbolic geometry relates to life and the double-helix model of development.  The model does rely on the traditional metaphysical relationship between transcendence and immanence (the relationship between source and manifestation).  Immanence starts metaphorically from the ground and builds up.  Transcendence starts metaphorically from the sky (what new atheists call “sky hooks”) and reaches down.  Now, just as spinning strong thread involves twisting fibres around each other, so double (and triple, etc.) spirals strengthen the reach of each fibre.  Metaphorically speaking, this strengthening allow the immanent to reach closer to the transcendent and the transcendent to reach further into the immanent.  As an example, consider these illustrations where the wind-sock illustrates the double helix model and the morning glory vines illustrate the reality of life in immanence reaching for the sun.

 

 

 

 

 

 

 

 

 

 

So the double-helix sets the ideal pattern while the vines strive to reach their potential.  Stay tuned for more adventures in Hyperbolic Geometry!

 

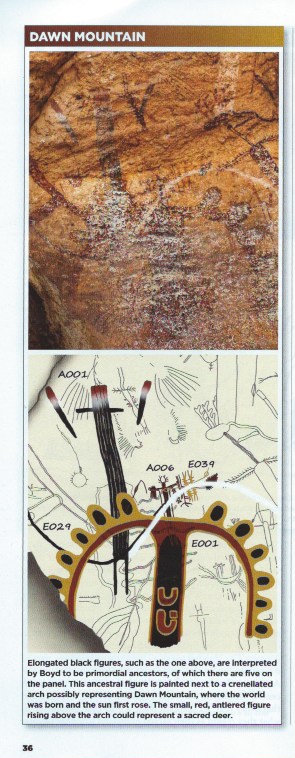
Next adventure:  Mesoamerican shamans 5,700 years ago painted what is now considered to be a creation story in a cave at Dawn Mountain in Texas.  The “White Shaman rock shelter” has been painstakingly studied and recreated by artist turned archaeologist Carolyn Boyd.  In this rendition of a portion of the painting, “[an] ancestral figure is painted next to a crenellated arch poorly representing Dawn Mountain, where the world was born and the sun first rose.”  (Archaeology, Nov./Dec. 2017, “Reading the White Mountain Mural” by Eric A. Powell, pg. 36.)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Future Adventures:  Is the Universe Crenellated?

This seems to me a good synopsis of the perspective that  the universe is warped rather than vectored:

########################################################

“Lovely and creative translation from medium to medium, the correlate of science patterns and crocheting!  Thanks for letting me in on your musings and discoveries.”  — Dr. Susanne Cook-Grueter, June 13, 2017.